Shāh māt
Published:
Chess and AI
“Shāh māt”: checkmate at the crossroads of chess and inference
“Shāh māt” is often glossed as “the king is dead” in Persian—the phrase we borrow in chess for a final, inescapable attack.
Take Take Take is an innovative platform for tracking tournaments and streaming live games. Recently, they ran a fun challenge—hosted on Kaggle—to crown the best AI chess player among large language models (LLMs). In short: which LLM could beat other LLMs at chess?
As a lifelong AI tinkerer and chess fan, I’ve always wondered why LLMs stumble at serious over-the-board reasoning while specialist engines soar. (If you want an entertaining take, GothamChess has a great explainer: video.) This contest was the perfect excuse to dig deeper.

The three phases of chess
Chess is commonly divided into the opening, middlegame, and endgame. The phases aren’t just labels—they shape how we think.
Opening
The opening is about fast development, central control, and king safety—laying tracks for the game to run on. Because these positions repeat across games, opening theory is highly cataloged; many players “book up” on favorites (Sicilian, King’s Indian, Queen’s Gambit, etc.). The aim isn’t to win outright but to reach a playable middlegame with purposeful piece placement.

Middlegame
The middlegame begins once development stabilizes. It’s tactical, messy, and deeply positional: create weaknesses, seize open files, probe for king safety, and trade (or refuse to) on your terms. It’s where intuition, pattern recognition, and calculation collide. There’s no universal recipe; plans depend on the structure you steered into from the opening and the endgames you’re willing to play.
Endgame
The endgame is surgical. With material thinned, every tempo matters: activate the king, push passed pawns, and convert small edges. At serious levels, many games end with a resignation before the final checkmate—once conversion is technically inevitable. Endgame technique is precision chess.

Why the phases matter for AI
Sergey Levine (UC Berkeley) popularized a powerful lens: reinforcement learning as probabilistic inference. The idea is to cast control problems as graphical models where you infer actions that make an entire trajectory “optimal.” (I made summary slides for my Graphical Models course here. The foundational paper is here.)
A (very) short primer on graphical models
Graphical models describe dependencies between variables using nodes and edges. In RL, we model states \(s_t\), actions \(a_t\), and optimality variables \(O_t\) that “light up” when an action is good:
\[p(O_t=1 \mid s_t,a_t) \propto \exp\!\big(r(s_t,a_t)\big).\]Condition on every step being optimal, \(O^{*}_{1:T}=1\), and the inference problem asks: _Which actions make that likely?* The chain looks like
\[s_1 \to a_1 \to O_1 \to s_2 \to a_2 \to O_2 \to \dots \to s_T \to a_T \to O_T.\]Running sum–product (message passing) yields backward messages that behave like value functions and forward messages that behave like state visitation measures. The soft-optimal policy pops out as a softmax over state–action values:
\[\pi^*(a_t \mid s_t) \propto \exp\!\big(Q(s_t,a_t)\big), \qquad V(s_t)=\log \sum_{a} \exp\!\big(Q(s_t,a)\big).\]Why this view is useful
Treating control as inference unifies planning and uncertainty in one framework:
- Exploration emerges naturally via the softmax (maximum-entropy RL) rather than being bolted on (e.g., ε-greedy).
- Structure matters: messages respect the problem’s temporal and causal graph, so credit assignment and planning are principled, not heuristic.
State marginals: where forward meets backward
- Forward messages ( \(\alpha_t\) ): probability mass that reaches a state, given the past and rewards along the way.
- Backward messages ( \(\beta_t\) ): probability that from a state you can continue optimally to the goal.
- Their product gives the state marginal—how likely you are to occupy each state at time \(t\), given optimality.
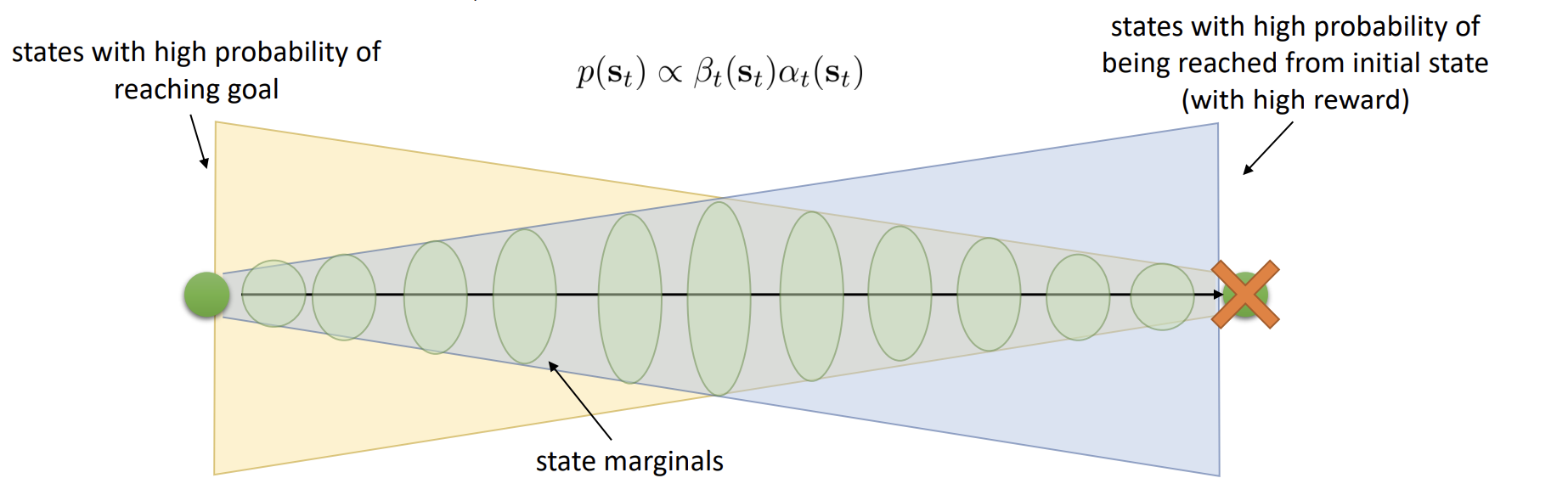
Now squint at chess through that lens:
- Opening ↔ forward messages: you push probability mass toward futures you want to inhabit (good structures, harmonious piece activity).
- Endgame ↔ backward messages: you reason backward from known wins (tablebase-like certainty, winning plans).
- Middlegame ↔ their intersection: the live negotiation between what’s reachable and what converts.
This is one reason LLMs struggle: they excel at patterned next-token prediction, but strong chess demands structured search with explicit value propagation over a combinatorial game tree.
Engines, search, and (a bit of) learning
Stockfish, briefly
Stockfish—arguably the strongest open-source engine—still centers on minimax with alpha–beta pruning, plus modern staples (iterative deepening, transposition tables, and smart move ordering). Its leap in recent years came from integrating NNUE (a compact, efficiently updatable neural evaluation). The network ingests sparse piece–square features and—thanks to incremental updates—can be queried at millions of nodes per second without sinking the search.
How are NNUE weights trained? In practice, supervised regression on vast corpora of positions labeled by deeper engine search (and self-play generation). The network learns to mimic those strong evaluations; during search, its predictions guide pruning and move ordering. The hybrid works: exhaustive tree search for tactical certainty, learned evaluation for positional nuance.

So where does RL fit?
Maximum-entropy RL—and the inference view above—gives us a mathematically grounded way to push and pull probability mass through time, exactly what chess planning needs. You don’t have to replace search; you can compose it with learned components and principled uncertainty handling. That’s the lesson from engines like Stockfish (and, in a different flavor, policy/value-guided systems): search thrives when paired with models that understand positionally “what tends to work.”
Closing
Graphical models give a clean story for how humans seem to reason across chess phases: projecting forward, reasoning backward, and meeting in the middle. LLMs shine at language; chess demands explicit structure. If you’re curious about the details, check out my summary slides here and the original paper here—and absolutely watch the GothamChess video.
I’d love to hear your thoughts, critiques, or follow-ups—especially ideas for experiments that tie state marginals to concrete chess plans. Hit me up.
